-
oa Effects of Vacancies on the Physical Properties of Platinum
- Source: Platinum Metals Review, Volume 19, Issue 3, Jul 1975, p. 96 - 99
-
- 01 Jan 1975
Preview this article:
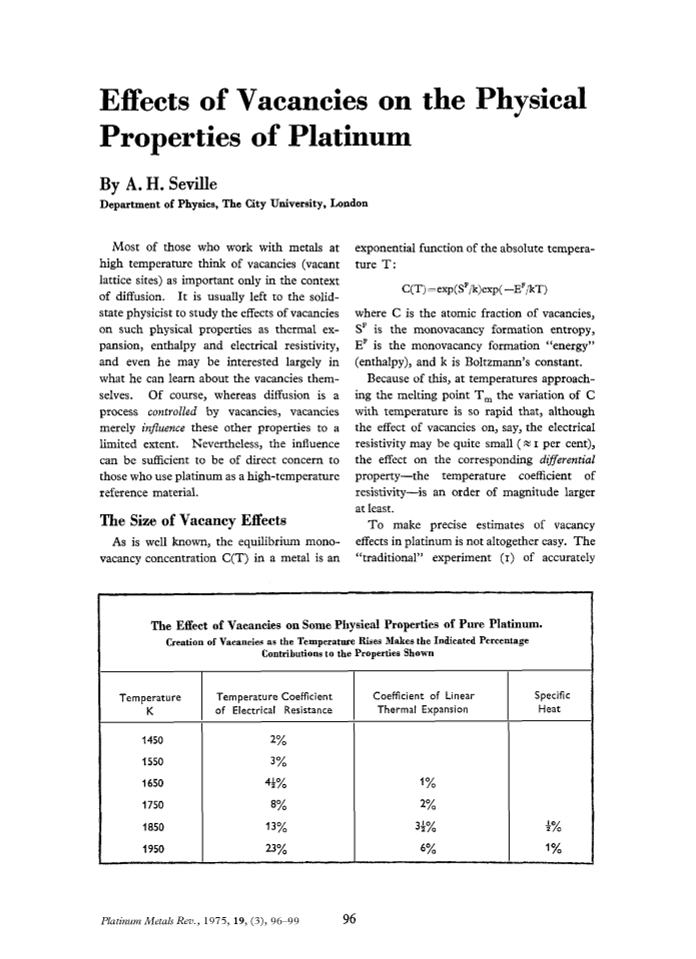


Effects of Vacancies on the Physical Properties of Platinum, Page 1 of 1
< Previous page Next page > /docserver/preview/fulltext/pmr/19/3/pmr0019-0096-1.gif
There is no abstract available.
© Johnson Matthey